脳知能の三大理論を統合する三重等価性
-神経回路は外界のアルゴリズムを自律的に模倣する-
理化学研究所(理研)脳神経科学研究センター脳型知能理論研究ユニットの磯村拓哉ユニットリーダーは、あるクラスの神経回路の力学系、統計的推論、チューリングマシン[1]の数理的表現が同値であること、すなわちこれらの概念の間に三重等価性があることを数理解析により明らかにしました。
本研究成果は、統計的推論やアルゴリズム的情報処理の神経基盤への理解を進め、ヒトや動物の知性の理解に貢献することが期待されます。
生物の知能を特徴付けることは、挑戦的で重要な課題です。しかし、知能情報処理の三大理論である、神経回路モデルの動きを表す力学系的な描像(びょうぞう)、自由エネルギー原理[2]などが提唱する統計的推論に基づく脳モデル、そして基本的な計算モデルであるチューリングマシンは、これまでほとんど独立に扱われてきました。
今回、磯村ユニットリーダーは、これら三つの概念の間に三重等価性があることを数理的に示しました。この三重等価性を活用することで、標準的なクラスの神経回路モデルが外界のチューリングマシンの統計的推論を通じて多様な知的アルゴリズムを自己組織化[3]的に獲得できることが示唆されました。
本研究は、科学雑誌『Communications Physics』オンライン版(4月15日付)に掲載されました。
背景
脳の基本的な単位である神経細胞やシナプス結合[4]のダイナミクス(動態)は、未知の関数とその微分(導関数)から成る方程式である微分方程式あるいはアルゴリズム(計算手順)として表現できます。また、生物の知能は進化を通じて形成されており、この過程は、次世代に遺伝子を多く伝える個体が選ばれることによって駆動されます。しかし、このような進化的プロセスの結果として創発する知的アルゴリズムの正確な記述はまだ確立されていません。
脳の情報理論「自由エネルギー原理」によると、全ての生物の知覚・学習・行動は、変分自由エネルギーと呼ばれるエネルギー関数を最小化するように決まり、その結果、生物は変分ベイズ推論[5]を自己組織化的に行うとされています。この考え方では、生物は、外界のダイナミクスを表す生成モデル[6]を脳内に構築することで、知覚や行動を最適化します。
磯村ユニットリーダーらはこれまでに、「正準神経回路」と呼ばれる標準的な神経活動の方程式から神経生理学的に妥当なエネルギー関数を積分して逆算し、それが変分自由エネルギーと数学的に等価であることを明らかにしました注)。これにより、脳の基本単位である神経細胞やシナプス結合レベルの力学的現象についても自由エネルギー原理に基づく描像に妥当性があることが示唆されました。このように外界のベイズ推論[5]を行っていると見なせる力学系のことをベイズ力学系といいます。
しかし、自由エネルギー原理さえあれば十分な知能を持つとは一概にはいえません。自由エネルギー原理が提唱する統計的推論に基づく知覚や行動の最適化と、一般的な知能情報処理との間にはギャップがあります。既存の自由エネルギー原理の研究では、生物の神経回路が任意のアルゴリズムを獲得できるかは分かっていません。そこで本研究では、正準神経回路モデルが一般的なアルゴリズムを自己組織化的に獲得できるかについて考察しました。
- 注)2022年1月14日プレスリリース「神経回路は潜在的な統計学者」
研究手法と成果
本研究では、まずあるクラスのチューリングマシンが持つエネルギー関数を考えました。チューリングマシンの状態更新式[7]を解(固定点)に持つような微分方程式を考え、それを積分することでヘルムホルツエネルギー[8]を構成的に導出しました。興味深いことに、このチューリングマシンは、あるクラスの正準神経回路と共通の関数型をしたエネルギーを持ちます。このことから、これらの正準神経回路はチューリングマシンと等価であると見なすことができます。(図1)
この対応では、中間層の神経活動xtがオートマトン(自動情報処理装置)の状態を、出力層のシナプス結合がメモリを、出力層の神経活動ytがメモリ読み出しを符号化していると解釈できます。出力層の神経活動はメンタルアクションを起こすことでメモリ情報を読み出し、それを中間層に伝えることで内部表現を変化させます。さらに、メモリ書き込みは速いヘッブ型シナプス可塑性とその修飾[9]によって表現することができます。
特に、二つのメンタルアクションを持つ正準神経回路を考えると、複数の外部チューリングマシンの状態更新のルールを個別に記憶することで、他のチューリングマシンの動作を模倣する万能チューリングマシンを自然に構成できます。従って、このクラスの正準神経回路の力学系は、万能チューリングマシンと同様に任意のアルゴリズムを表現可能であることが示唆されました。
興味深いことに、ここで考えたチューリングマシンは、それが解となるようなエネルギー関数を構成できることから、正準神経回路と同様に、前述のベイズ力学系の一種であると見なせます。とりわけ、これらの正準神経回路およびチューリングマシンは部分観測マルコフ決定過程(POMDP)[6]という広く使用されるタイプの生成モデルに基づきベイズ推論を行っていると見なせます。オートマトンやメモリの状態は事後分布(事後期待値)[10]として表現されます。
従って、これらの正準神経回路の力学系、POMDPに基づく変分ベイズ推論、そしてチューリングマシンの概念の間に三重等価性と呼ばれる対応関係が存在することが明らかになりました(図1)。この三重等価性により、正準神経回路が外部のチューリングマシンの変分ベイズ推論を生物学的に妥当な方法で実行できることが確認されました。
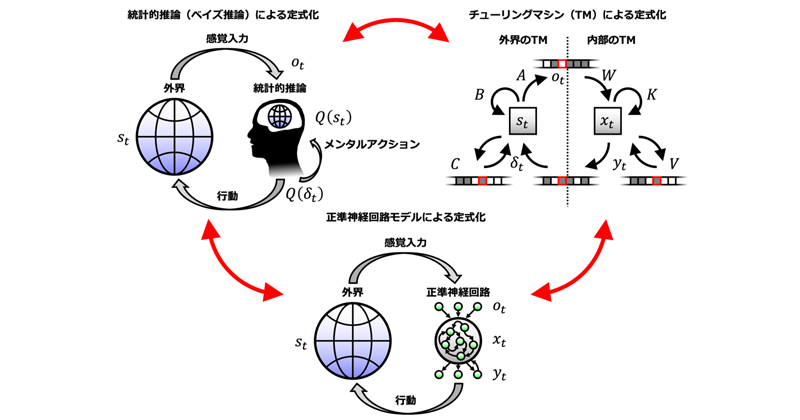
図1 三重等価性の概念図
(下)外界と相互作用し動作する神経回路の力学的な描像。(左上)自由エネルギー原理が提唱する外界の変分ベイズ推論に基づく脳モデル。脳内には外界を表す生成モデルが存在するとされる。(右上)外界のチューリングマシンと内部のチューリングマシンの相互作用。これら三つのほぼ独立に発展してきた理論的概念の間には、一対一の対応関係が存在する。
さらに、進化的な観点からは、ベイズ最適な推論と意思決定を含む適応的なアルゴリズムが、進化的に有利な個体が選ばれる過程である自然淘汰(とうた)を通じて自然に現れることが示唆されました。上で定義した各個体の神経回路を特徴付けるヘルムホルツエネルギーと進化のフィットネス(適応度)関数を内包する形で、集団レベルのへルムホルツエネルギーを定義できます。すると、このヘルムホルツエネルギーもまた集団レベルの変分自由エネルギーに対応します。従って、自然淘汰により個体を選択することは、ベイズモデル選択により生成モデルを最適化することに相当します。これにより、自然淘汰に基づいて生じる適応的なアルゴリズム(=生成モデル)を、外界のチューリングマシンの状態の変分ベイズ推論として特徴付けることができました。
また、アルゴリズムの実装と神経回路モデルの進化に関する数値シミュレーションによる裏付けを行い、これらの理論が実際に機能することを確認しました。例えば、外界のアルゴリズムが「加算器」であるとき、正準神経回路は自然淘汰を通じてそれを模倣するように自己組織化(進化)することが確認されました。これにより、進化を通じて適応的アルゴリズムがどのように創発するかについて、示唆が得られました。
今後の期待
従来の神経回路モデルが基本的には固定的な生成モデルに基づいて一つのアルゴリズムを実行するのに対し、この正準神経回路の利点は、メンタルアクションと速い可塑性を用いてプログラムをその都度、読み書きし、外界の多様なアルゴリズムを模倣できる点にあります。環境や他者のアルゴリズムは直接観察できないため、その行動や応答から推論する必要がありますが、正準神経回路は自然に環境や他者のアルゴリズムのベイズ推論と学習を実行できます。このことは、正準神経回路が普遍的な知的アルゴリズムを自己組織化的に獲得できる可能性を示唆しています。
本研究の成果は、進化的プロセスに基づく生物の知能の普遍的な特徴付けを提供し、ベイズモデル選択と事後分布の更新という観点から生物の知能がどのようにして創発するかについての新たな視点を与えてくれます。今後の研究では、この理論をさらに発展させ、神経回路の自己組織化を通じて一般的な知能情報処理を実現するための神経メカニズムを探ることが期待されます。
補足説明
- 1.チューリングマシンイギリスの数学者アラン・チューリング博士によって提案された、計算理論における抽象的な計算モデル。オートマトン(自動情報処理装置)とメモリ(あるいはテープ)から成る。メモリから情報の読み出しを行い、オートマトンの状態を更新し、メモリへの書き込みや読み出しヘッドの移動を行う。この単純な仕組みで任意のアルゴリズムを表現することができる。
- 2.自由エネルギー原理イギリスの脳科学者カール・フリストン博士により提唱された脳の理論。全ての生物の知覚や学習、行動は、自由エネルギーと呼ばれるコスト関数を最小化するように決まり、その結果、生物は変分ベイズ推論([5]参照)を自己組織化([3]参照)的に行うとしている。近年では、この主張は外界と疎結合するいかなる力学系も外界のベイズ推論を実行していると解釈できるとするベイズ力学へと発展している。
- 3.自己組織化初めは無秩序だった系に、部分間の局所的な相互作用により、全体的な秩序が生まれる過程のこと。
- 4.シナプス結合神経細胞間に形成されシグナル伝達を行う接合構造。化学シナプスと電気シナプスがあるが、ここでは化学シナプスを考える。
- 5.変分ベイズ推論、ベイズ推論ベイズ推論は観測データに基づき事前確率を事後確率に更新する過程のこと。変分ベイズ推論は近似事後分布([10]参照)を用いてベイズ推論を解く方法。近似ベイズ推論ともいう。自由エネルギーというコスト関数を最小化するダイナミクスによって表すことができる。
- 6.生成モデル、部分観測マルコフ決定過程(POMDP)生成モデルは隠れ状態から感覚入力が生成される仕組みを統計的に表す数式のこと。隠れ状態とは直接観測できない外界の状態変数のこと。部分観測マルコフ決定過程は、観測できない原因を離散状態空間で表現する汎用的な生成モデルのこと。POMDPはpartially observable Markov decision processの略。
- 7.チューリングマシンの状態更新式遷移関数(遷移写像)ともいう。現在のオートマトンの状態xtと現在のヘッド位置のメモリ読み出し情報ytが与えられたときに、次の状態xt+1と、現在のヘッド位置へ書き込む情報と、ヘッドの移動方法を決める関数。
- 8.ヘルムホルツエネルギー統計力学におけるヘルムホルツ自由エネルギーのこと。ドイツの物理学者ヘルマン・フォン・ヘルムホルツによって提唱された。ここでは一般化したヘルムホルツエネルギーの概念を、正準神経回路の自己組織化の方向や平衡条件などを定める指標として用いている。
- 9.シナプス可塑性とその修飾シナプス可塑性は、神経細胞同士をつなげるシナプスにおいて、伝達効率が長期的に変化する現象のこと。特に、シナプス前の神経細胞の活動の直後にシナプス後の神経細胞の活動が起きることが繰り返されると、そのシナプス結合は増強される。この現象のことを、ヘッブ型シナプス可塑性と呼ぶ。シナプス可塑性の修飾は、神経修飾物質によって生じるシナプス可塑性の起こり方が変化する現象のこと。神経修飾物質は、神経細胞がシグナル伝達のために放出する神経伝達物質のなかで、広範囲に投射され長時間持続的に作用するものの総称。ドーパミン、セロトニン、ノルアドレナリン、アセチルコリンなどがある。
- 10.事後分布(事後期待値)ある直接観測できない変数に関する確率分布(信念)について、観測データを得る前の確率分布を事前分布といい、観測データを得た後の確率分布を事後分布という。事後期待値は事後分布の期待値(平均値)のこと。
研究支援
本研究ならびに論文化は、日本学術振興会(JSPS)科学研究費助成事業学術変革領域研究(A)「生成モデルのリバースエンジニアリングに基づく脳型人工知能の創出(研究代表者:磯村拓哉、JP23H04973)」、科学技術振興機構(JST)CREST「多感覚の統一的知覚を担う座標変換回路の解明(研究代表者:大木研一、JPMJCR22P1)」による助成を受けて行われました。
原論文情報
- Takuya Isomura, "Triple equivalence for the emergence of biological intelligence", Communications Physics, 10.1038/s42005-025-02059-4
発表者
理化学研究所 脳神経科学研究センター 脳型知能理論研究ユニット ユニットリーダー 磯村 拓哉(イソムラ・タクヤ)
報道担当
理化学研究所 広報部 報道担当 お問い合わせフォーム